ニュース&イベント NEWS & EVENTS
2つの独立した全結合型イジングマシン実装により相互作用数半減手法効果を実証
~ホップフィールドネットワークの課題を克服、エッジで組み合わせ最適化問題を解く~
研究の要旨とポイント
- ホップフィールドネットワークは組合せ最適化問題の解を得られるものの、局所解に陥りやすいという問題があります。全結合型イジングマシンは、そうした課題に対応できる機構です。
- 今回、これまでに研究チームが開発したスケーラブルな全結合型イジングマシンのボード上に、2つの独立した 384 スピン全結合型イジングマシンを実装することに成功しました。これにより、相互作用数を半減させることができます。
- 本技術により、エッジ側での大規模化が可能となり、組合せ最適化問題のより効率的な求解処理が実現できると期待されます。
研究の概要
東京理科大学 工学部 電気工学科の河原 尊之教授らの研究チームは、2つの独立した全結合型イジングマシン実装により、相互作用数を半減する手法の効果を実証しました。この技術を活用することで、エッジ側での大規模化が可能となり、社会に広がる組み合わせ最適化問題を高速かつ低消費エネルギーで解くことができるようになると期待されます。
深層機械学習へ繋がる先駆的な技術として2024年度のノーベル物理学賞の対象となったホップフィールドネットワークですが、ニューラルネットワークモデルそのものとしても非常に有用な技術です。全結合型イジングマシンとは、ホップフィールドネットワークに量子Inspired技術であるアニーリング機構を組み込んだものであり、物流・通信網・金融・創薬など社会に広がる組合せ最適化問題の求解をその場で低電力かつ高速に実行できます。
今回、研究チームは、全結合型ではスピン数の2乗個必要な相互作用回路について、アレー回路の2次元配置に規則性を持たせることで、スケーラブル構造と親和性が高い相互作用数半減手法を提案しました。デモとして、2022年3月に報告した16 個のFPGAチップによる 384 スピン全結合型イジングマシンのボード(※1)上に、2つの独立した 384 スピン全結合型イジングマシン(すなわち384スピン×2個であり、かつ独立に動作)を実装することに成功しました。
※1「量子Inspired技術の新展開:スケーラブルな全結合型イジング半導体システム ~組み合わせ最適化問題求解を低消費電力かつ高速に行う技術の基礎検証に成功~」
本研究成果は、2024年10月1日に国際学術誌「IEEE ACCESS」にオンライン掲載されました。
研究の背景
配送ルートの最適化から金融ポートフォリオ決定、創薬・新素材開発まで、組合せ最適化問題(*1)は社会に多数存在しています。交通経路や物流コストの最適化、通信や電気エネルギー網の最適化などは、デジタル田園都市構想が掲げる地域の持続的発展にも繋がることから、組合せ最適化問題を効率的に解くことが求められています。しかしながら、組合せ最適化問題の解法として、すべての状態を総当たりで調べる方法では、候補数(例えば物流での配送先数)が増えると必要な時間(計算量)が指数関数的に増大することから、実用的ではありません。
一方で、組合せ最適化問題における最適な解との差をエネルギーとして捉えなおすと、相互全結合型ニューラルネットワークのひとつであるホップフィールドネットワーク(*2)として記述することができます。そして、このネットワークが持つエネルギーを小さくする機能を用いることで、組合せ最適化問題の解を得られることを、ホップフィールドらが1985年に示しました。これらのエネルギーの最低値が、組合せ最適化問題の最適な解となるのです。この手法では候補数が増えてもこれに比例する程度の計算量となり、飛躍的に高速に解を得ることができます。これはまた、磁性体のモデル(イジングモデル、*3)のエネルギーの式から動作を決める方式にも繋がりました。
しかし、ホップフィールドネットワークには課題もありました。原論文でのホップフィールドネットワークでは、真の最小値ではなく、局所的な小さな値(局所解)で変化が止まってしまう場合があるのです。これを改善するため、状態変化を確率的な動作として、あるいは温度によってこの動作を変化させる機能を組み込んで局所解に陥りにくくしたものが、全結合型イジングマシンです。
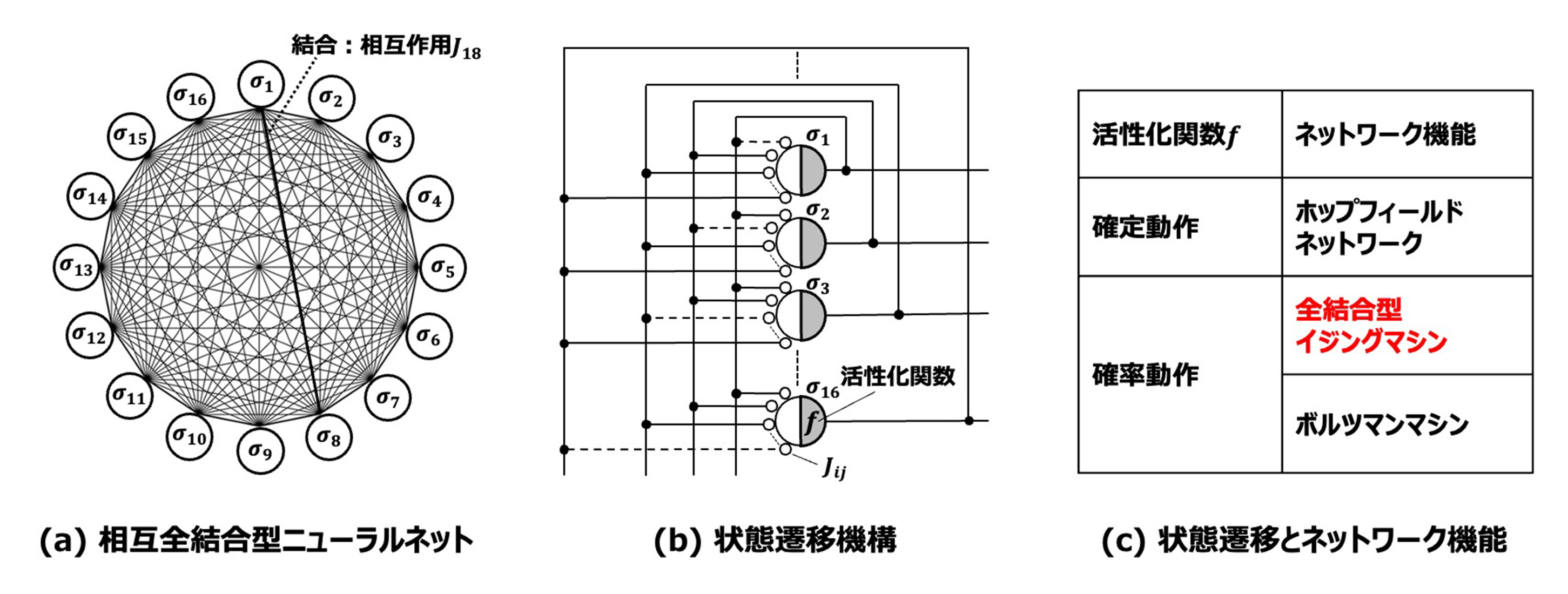
図1. 相互全結合型ニューラルネットワークの構造とそのスピン更新(状態遷移)機構。
(a)要素であるスピンσi(i=1∼16)があり、任意の2つのスピン間に双方向の相互作用Jij(図ではi=1,j=8を太線で表示)がある。(b)スピンσiの値は2値をとるが、その更新を∑jJijσjの値を元に活性化関数で行い、ネットワークのエネルギーが下がる方向へ状態が遷移していく。(c)状態遷移の機構(b)において、その動作が確定動作か確率動作かでネットワークの遷移が異なる。
相互全結合型ニューラルネットワークの構造は図1(a)のようになり、組合せの要素として上向きまたは下向きの二つの状態をとるスピンσiと、任意の2つのスピン間の双方向の相互作用Jijでの結合(全結合型)によって記述できます。Jijは、2つのスピンの双方向の結合の強さであり、組合せ最適化問題では、特定の組合せの実現しやすさに対応します。また、図1では簡略化のため省略していますが、組合せの要素の重要度や影響力を加味するために、イジングモデルから外部磁場hiを導入します。
このネットワークのエネルギーは、E=-∑i,jJijσiσj-∑ihiσiと表され、このEを小さくするようにスピンの状態を更新する機構を組み込むことで、最低値になった時のスピンの値の組を得ることができます。これが、組合せ最適化問題の解となります。相互全結合型ニューラルネットワークでは、スピンσiとσjをEを小さくする方向への計算が主体となり、膨大な数となるすべての組合せを総当たりで計算することはしないことから、効率的な計算が実現できます。また、これらの動作では並列化の工夫ができることから、大幅な高速化が可能となります。
この更新する機構を示したものが、図1(b)です(ネットワークの構造としては(a)と(b)は同じ)。σiの更新を決定するには、まず、∑jJijσjの値を求める必要があります(実際はhiも考慮)。この積和計算は一クロックで行うこともできます。この結果を元に、あるしきい値を定めて、積和計算の値と比較してσiを更新するか否かを判断します。このとき、 図1(c)で示したように、値の比較のみで確定させる動作とするのが、ホップフィールドネットワークです。これは歴史的に極めて重要な成果でしたが、前述の通り、真の解ではなく、局所的な小さな値で変化が止まってしまう場合もありました。これを解決するため、この更新判断に確率的な動作を導入したものが、その後の深層学習へ繋がるボルツマンマシンであり、更新を温度によって変化させるものが全結合型イジングマシンです。
全結合型イジングマシンのエッジ側でのLSI実装について、東京理科大学工学部電気工学科は大規模化を継続的かつ系統的に推進してまいりました。2016年、国際学会IEEE NEWCASにて提案した全結合型でのLSI構成を皮切りに、2020年には、積和計算を並列で行うことを電力性能比向上への強みとするLSI実装方式にて単一チップへ全結合型を組み込みに成功(国際学会IEEE SAMIにて発表、※2)し、更に、2022年3月及び2024年1月には、複数チップでの一体化全結合動作可能なスケーラブル構造を提案し実証した結果を報告しました(同IEEE SAMIにて発表、※3)。これらの背景のもと、スピン数の2乗個となる相互作用実現回路数の削減が課題となり、今回、検討を深めました。
※2「世界で初めての全結合型半導体アニーリング方式人工知能チップを開発 ~512スピン実装により22都市巡回セールスマン問題求解を瞬時に (ノイマン型高性能CPUではおよそ1200年が必要)~」
※3「22nm CMOSチップを用いたスケーラブルな全結合型半導体イジングプロセッシングシステム ~組み合わせ最適化問題を低消費電力かつ高速に解く技術の大容量化にめど~」
研究結果の詳細
-
今回の提案手法
イジングマシンで解ける問題の規模はスピン数に依存します。実社会におけるさまざまな問題を解くためにはスピン数を増やしていくことが求められますが、全結合型では相互作用がスピン数の2乗個必要となります。これが、大規模化を阻む大きな課題となります。
低電力で高い演算性能を得るための有望な方法として期待されるのが、多数の並列動作です。多数の並列動作では、LSI上に相互作用Jijを実現した各要素回路を配置することから、i行j列の2次元のアレー状に配置されることになります。この形態はコンピューティングインメモリにも繋がります。しかしながら、全結合型の相互作用Jijは多数であり、LSIチップ実装においてはこれに対応する回路部分の面積がチップ面積の大部分を占めてしまうことになります。これが、大規模化に向けた課題となります。
そこで、河原教授らは、2つの方向からこの問題にアプローチしてきました。ひとつは複数のチップを用いながらひとつの全結合型イジングマシンとして動作させるスケーラブル化と、もうひとつは、相互作用要素回路の個数を削減することです。
スケーラブルな全結合型イジングマシンの開発は、これまでの研究からある程度実用化に向けためどをつけることができています(過去のプレスリリース※1〜3参照)。こうした研究を礎に、今回、アレー状の回路の2次元配置に規則性を持たせることで、スケーラブル構造にも親和性が高い相互作用数半減手法を提案しました。
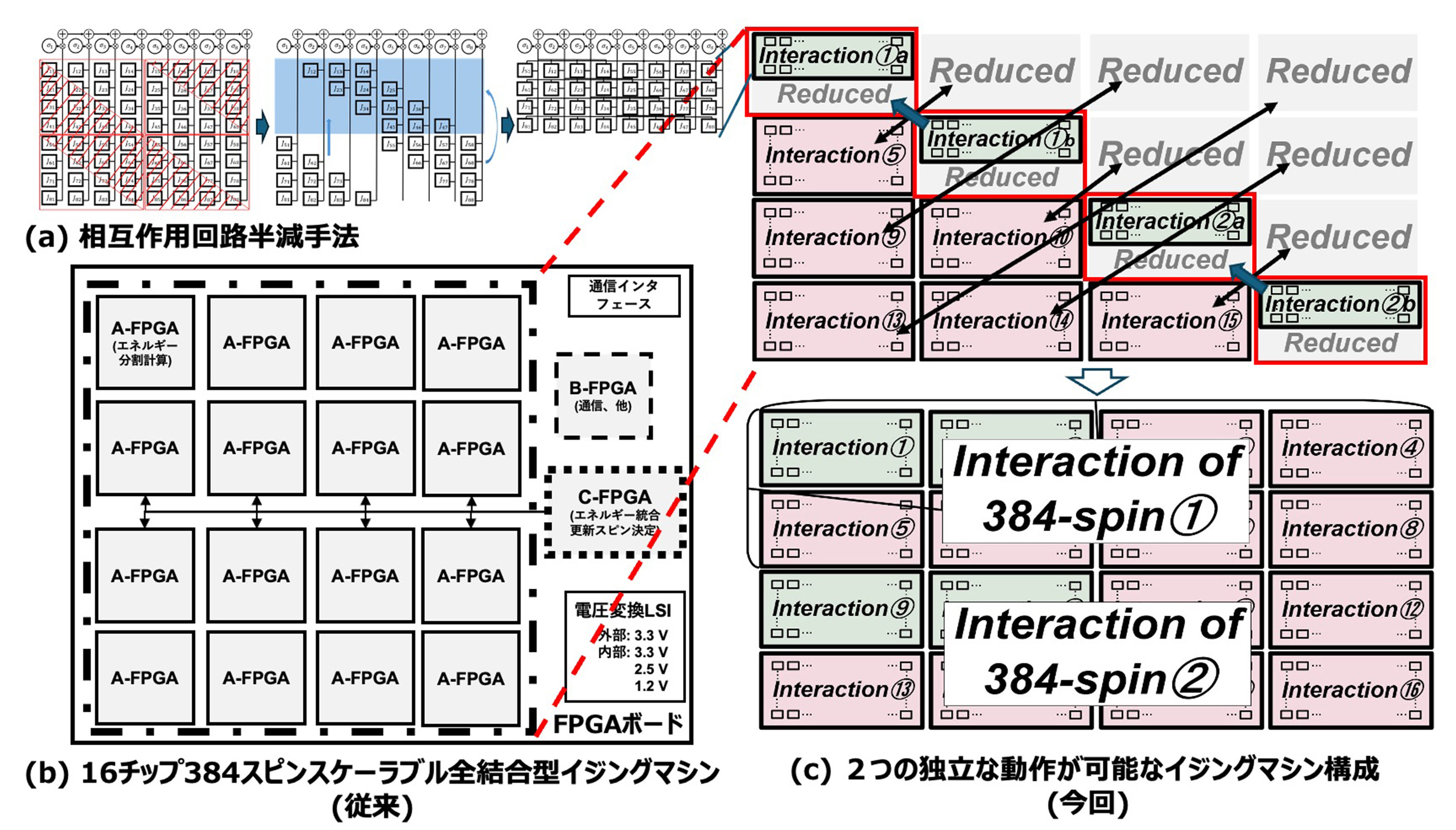
図2. 今回開発した相互作用回路半減手法。規則性を持ちスケーラブル構造と親和性が高い。(a)相互作用回路アレーを4つに分割し2次元配置に規則性を持たせた相互作用回路半減手法。(b)従来の16チップを用いた384スピン全結合型イジングマシンのFPGAボード構成図。(c)スケーラブル構造と合わせた相互作用回路半減手法と、2つの独立した動作が可能な384スピン全結合型イジングマシンの構成。
まず、 イジングマシンの相互作用行列においては、次の式が成り立ちます。
{Jij=0(i=j)
Jij=Jji(i≠j)
上記を相互作用の行列と見立てると、対角にある成分はすべて削除することができ、それ以外の成分も重複するペアのうち片方を削減することができます。これはネットワークの定義からは自明です。しかし、いざLSI上にJijの各要素回路を配置する方式では、これらをそのまま取り除くことは難しく、そのアレーで回路を配置した結果は三角形となってしまいます。
2020年1月発表に発表した方式(※2)では、相互作用回路を半減させて残った回路を、折り畳んで矩形として配置したため、削減後の相互作用の行列としての並びが複雑になってしまうという問題がありました。そのため、スピン更新の計算においてi行目の相互作用をすべて読み出すための制御や配線も複雑になってしまい、スピン数の拡張やハードウェアへの実装が困難であるという課題がありました。
この課題を解決するために、今回、図2(a)に示したように、相互作用行列を4つに分割し、まず分割されたそれぞれのブロックにおいてJij=0(i=j)またはJij=Jji(i≠j)を活用して約半分の削減を行いました。その後、残った相互作用を上下で組み合わせ矩形の形とする方式を採用しました。この方式では、相互作用行列の並びに規則性を残しながら半分を削減することができました。これは、削減後の相互作用回路を用いてスピンσi更新のためのエネルギー計算に必要な相互作用を読み出す方法にも規則性を残すことができることを意味しています。
これを元に、(b)に示した2022年3月に発表したFPGA(*3)を16チップ用いた384スピンスケーラブルイジングマシンボード(※1)を用いて、チップ数半減させたシステムをデモとして実装しました。ここでは(c)に示したように、この16チップに分割した相互作用行列の対角成分が含まれているものと含まれていないもので別々の方法で相互作用の半減を行います。対角成分が含まれているものは(a)の方式で半減し、次に、対角成分が含まれていないものでは転置行列のペアとなるチップが存在するため、片方を削減することができました。
この手法によって、カスタムLSIでの実装を想定して、FPGAの使用率を上げずに、384スピンを8チップで実装することができました。すなわち、従来(※1)と同じ規模の2つの独立した全結合型イジングマシンを同じボードに実装することができました。
-
評価結果
今回開発した2つの独立した384スピン全結合型イジングマシンの性能を評価するため、最大カット問題(Max-cut problem)と四色塗分け問題(Four-color problem)という2つの組み合わせ最適化問題を一度に解きました(図3)。
最大カット問題はあるグラフのノードを二つのグループに分ける場合にエッジを切る数が最大となる分け方を求めるという問題です。16×24のピクセル上に配置されたスピン値の1と-1をそれぞれ白と黒に対応させ、イジングマシンのエネルギー収束時にその白黒で指定の文字列を形成させるように設定しました。ネットワークとしての記憶機能を用いているのが特徴です。ここでは「TUS」(東京理科大学の英語名Tokyo University of Scienceの略語)の文字列を形成させるように問題の設定を行いました。
四色塗分け問題では、384スピンの規模の検証のための題材として、夏目漱石の『坊っちゃん』において、その舞台となった松山市を含む四国地方の市町村を四色で隣り合う事なく塗分けるという問題を選びました。『坊っちゃん』の主人公は東京理科大学の前身である東京物理学校を卒業し、松山市に教師として赴任した設定となっています。
この結果、今回の2つの独立した384スピン全結合型イジングマシンは、CPU(Core i7-4790)でイジングマシンを模擬してこの2つの問題を順次解いた場合と比較して、電力性能比が約400倍優れていることがわかりました。
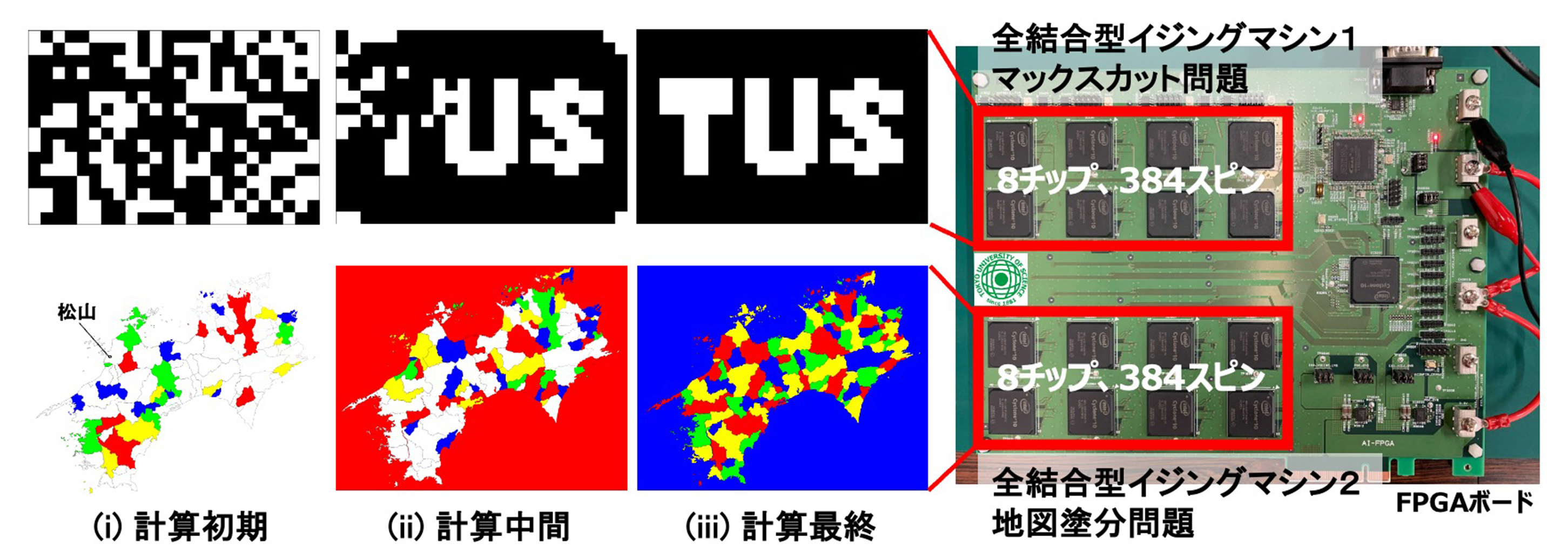
図3. 評価結果。2つの独立した384スピン全結合型イジングマシンを用いて、最大カット問題(Max-cut problem)と四色塗分け問題(Four-color problem)を同時に求解。
※本研究は、日本学術振興会科学研究費補助金(22H01559, 23K22829)の助成を受けて実施したものです。
用語
*1 組合せ最適化問題
選べる組合せの中から、与えられた条件を満たす一番良いものを探し出す問題。
例えば、巨大倉庫内の商品配置や荷物のピッキングのルートの最適化を考えてみよう。まず、倉庫内の商品配置においては、商品の取り扱い頻度や倉庫内の空間利用効率を考慮しながら、最適な配置を計画する必要がある。これは、ピッキングや出荷作業の効率化を図るための組合せ最適化問題となる。また、日々の作業効率のみで無く、この倉庫施設の保守管理においては、機器の稼働状況や故障のリスクを考慮しながら、最適な点検スケジュールやメンテナンス計画を策定する必要がある。これも機器の安定稼働を確保すると同時に、労力や時間を最小限に抑えるための組合せ最適化問題となる。さらに広げて施設の拡張や改修計画まで考えると、既存の施設設備やリソースの制約条件を考慮しながら、将来の需要を満たすための最適な投資計画を策定する必要がある。これもまた、限られた予算や施設スペースの中で、最適な機器配置や施設レイアウトを決定する組合せ最適化問題となる。
このような場合、まず最小単位である2つの要素間の選択を行うか否かを決めるが、この片方は、他の要素との関係でその選択を変えざるを得なくなり、そうした要素同士の関係による効果も考慮に入れる必要がある。そのため、全体としてある指標・条件で最適化するためには、大変な労力になる場合が多い。
*2 ホップフィールドネットワーク
1982年の論文で示された単層の再帰的な相互結合型ニューラルネットワーク。このネットワークでは、ニューロン間の重みにより、エネルギーが低い安定した状態として情報を記憶することができることも示し(ネットワークとしての記憶機能)、連想記憶への応用が示された。更に、組合せ最適化問題を解けることが1985年の論文で示された。提唱したジョン・ホップフィールド氏は「人工ニューラルネットワークによる機械学習を可能にした基礎的発見と発明に対する業績」として、ボルツマンマシンを提唱したジェフリー・ヒントン氏と共に2024年ノーベル賞受賞者となった。
*3 イジングモデル
二つの状態をとるスピンが格子点に配置され、最隣接するスピン間の結合を考慮する模型。強磁性体のふるまいを説明できる。
*4 FPGA
Field Programmable Gate Array。予め用意された論理回路の組み合わせを製造後に変えることができ、所望の機能を実現できるLSI (半導体集積回路)。
論文情報
雑誌名
IEEE ACCESS
論文タイトル
Implementation and Evaluation of Two Independent Ising Machines on Same FPGA Board by Reducing Number of Interactions Inside Ising Machine
著者
Shinjiro Kitahara, Taichi Megumi, Akari Endo, Takayuki Kawahara
DOI
※本論文はオープンアクセスです。自由にダウンロードし、お読みいだけます。
発表者
- 北原 伸次朗
- 東京理科大学大学院工学研究科電気工学専攻 修士課程2022年度修了 <筆頭著者>
- 惠 太一
- 東京理科大学大学院工学研究科電気工学専攻 修士課程2023年度修了
- 遠藤 あかり
- 東京理科大学大学院工学研究科電気工学専攻 修士課程2023年度修了
- 河原 尊之
- 東京理科大学工学部電気工学科 教授 <責任著者>
関連国際学会
学会名
IEEE Asian Solid-State Circuits Conference (A-SSCC 2022)
論文タイトル
Method of Halved Interaction Elements with Regularity Arrangement that achieves Independent Double Systems for Scalable Fully Coupled Annealing Processing
著者
Shinjiro Kitahara, Akari Endo, Taichi Megumi, and Takayuki Kawahara
DOI
10.1109/A-SSCC56115.2022.9980631
発表日
2022年11月8日(火)
関連書籍
「人工知能チップ回路入門」(河原尊之著、コロナ社、2024年10月刊行)
第7章と第8章で全結合型イジングマシンと関連技術を解説、第3章ではホップフィールドネットワークとボルツマンマシンを簡単に解説。
