-
数学科の特徴1
丁寧な指導と
充実のカリキュラム研究の最先端で活躍している第二部専任の教員が授業を担当し、きめ細かな教育を行っています。数学基礎力を育み、論理的に思考する態度と能力を養成するとともに、マルチメディア時代に対応する情報数学も修得できる充実したカリキュラムを構築しています。
-
数学科の特徴2
専門分野を
さらに深める道も4年次には解析学、代数学、幾何学、位相数学、確率論・統計学、離散数学、教育数学の分野に分かれ、卒業研究に取り組みます。また、理学部には専攻科(夜間)や大学院が設置されており、いっそう高度な技術者、教育者、研究者へと進む道も用意されています。
-
数学科の特徴3
教員養成の
伝統と実績本学科では、中学校教諭1種免許状(数学)、高等学校教諭1種免許状(数学・情報)の3つの教員免許を取得することができます。これまでに多数の教員を社会に送り出してきた伝統があり、教員志望の学生が毎年多く集まります。採用試験に関する情報交換も活発です。
基礎情報・資格 BASIC INFORMATION & CERTIFICATION
| キャンパス | 取得学位 | 在籍学生総数 | 目指せる資格 |
|---|---|---|---|
| 神楽坂キャンパス | 学士(理学) |
563名 男子 83%/女子 17% ※2024年5月1日現在 |
・中学校教諭1種免許状(数学) ・高等学校教諭1種免許状(数学・情報) ・測量士/測量士補 |
カリキュラム CURRICULUM
■必修科目 ◆選択科目
| 1年次 | 2年次 | 3年次 | 4年次 | |
|---|---|---|---|---|
| ■情報数学A・B/数学概論 ◆数学基礎A・B |
■プログラミングA・B ◆計算数学1A・1B/数学研究A・B/情報とマルチメディア/情報処理 |
◆計算数学2A・2B/データ処理A・B/情報表現技術/情報通信の科学/情報科教育法1・2/情報システム概論/ネットワーク概論/情報ネットワーク基礎/情報数学研究A・B/数学史/数学のための英語A・B/システムアドミニストレータ入門 |
■卒業研究 | |
| 解析学分野 | ■解析学1 | ■解析学2 ◆解析学研究/微分方程式A・B/複素解析A・B |
◆実解析A・B/関数解析A・B/解析学3A・3B | |
| 代数学分野 | ■代数学1 | ■代数学2 ◆代数学研究 |
◆代数学3A・3B/代数学4A・4B/代数学特講A・B | |
| 幾何学分野 | ■幾何学1A | ◆幾何学1B・1C/幾何学研究A・B/幾何学2A/応用解析A・B | ◆幾何学特講1A・1B/幾何学特講2A・2B/微分幾何入門A・B/多様体の幾何A・B | |
| 位相数学分野 | ◆位相数学1A・1B/位相数学研究A・B | ◆位相数学2A・2B/位相数学特講1A・1B | ||
| 確率論・統計学分野 | ■統計学1 ◆統計学研究/データサイエンス入門/データ解析入門 |
◆統計学2A・2B/応用統計学A・B/計算機統計学A・B/統計学特講A・B/データサイエンスA・B | ||
| 離散数学分野 | ◆離散数学1A・1B | ◆離散数学2A・2B | ||
| 教育数学分野 | ◆教育数学特講1A・1B/数学科教材研究A・B/数学科指導法1・2/数学科教育論1・2 | |||
2024年度 学修簿 卒業所要単位表
| 専門科目 | 基礎科目 | 一般教養科目 | 合計 | |||||
|---|---|---|---|---|---|---|---|---|
| 必修 | 選択 | 専門基礎 | 基幹基礎 | 関連専門 基礎 |
必修(外国語) | 選択必修(外国語) | 選択 | |
| 22 | 50 | 15 | 7 | 4 | 4 | 4 | 18 | 124 |
卒業研究・
研究室紹介
GRADUATE RESEARCH AND LABORATORIES
- ■解析学分野
- 解析学はアルキメデスにその片りんが見られますが、17世紀の微分積分学の誕生以来本格的に発展しました。現在では、微分積分を普通の関数よりも広い対象にまで拡張して、さまざまな問題の解決に取り組んでいます。
- ■代数学分野
- 代数学では、ベクトル空間、群、環、体など、何らかの演算が与えられている集合の性質を調べます。代数学はいろんな数学の“言葉”であるともいえます。例えば、定規とコンパスで角の3等分はできないことや、ボールと浮き輪が異なるといったことも代数を用いて厳密に記述することができます。
- ■幾何学分野
- 幾何学はある変換族によって不変な図形の性質を調べるクラインの幾何に始まり、その後、一般相対性理論と融合してリーマン幾何学、ローレンツ幾何学、さらにシンプレクティック幾何学に発展しました。
- ■位相数学分野
- ユークリッド空間の点と点同士が近いか遠いかという概念は距離を用いて記述でき、これによって写像の連続性が議論できます。このような概念を一般化したものが位相空間論です。また、位相幾何学では、連続変形で不変な図形の持つ性質を調べます。
- ■確率論・統計学分野
- 一見無秩序な現象でも、何度も起こると規則性が現れることがあり、これは調査や予測に生かせます。またブラウン運動のように無秩序な力が絶えず加わる運動は、方程式から法則性を解明できます。
- ■離散数学分野
- 離散数学の中のグラフ理論や離散幾何などを扱います。広く工学的な応用がなされている分野ですが、純粋数学的なアプローチで研究をしていきます。また、基本的には予備知識が必要ないことから、中学生や高校生にも理解させることが可能です。このメリットを生かして教育の中に離散数学を効果的に導入する方法なども考えます。
- ■教育数学分野
- 数学教員になるには、まず深い数学の理解が重要です。新鮮な数学的成果を教育の場で反映させるためには、教員が自ら数学研究を続けなければなりません。数学教育の実践的手法を学ぶ一方で、数学研究を生涯続けていく土台作りを目指します。
学生の声 VOICE
進路 CAREER
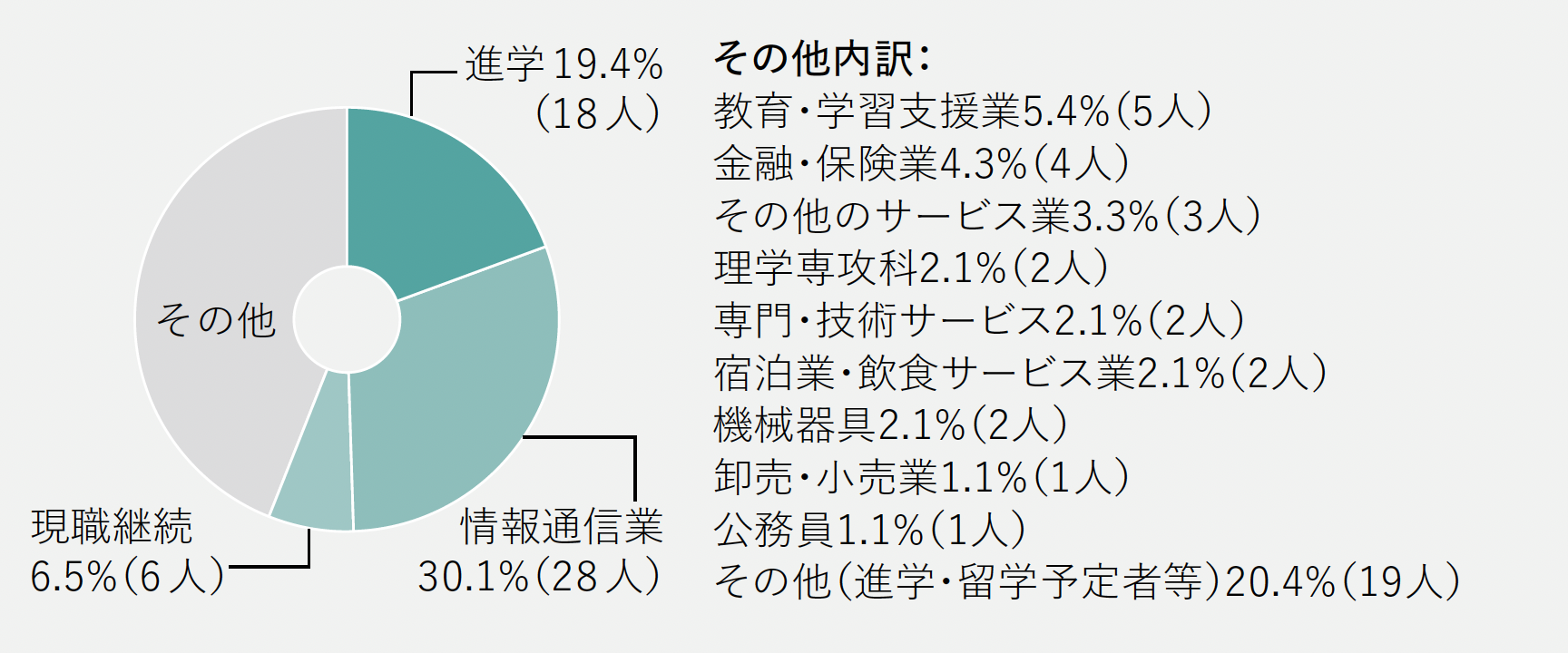
2024年3月31日現在
主な就職先
-
[情報通信業]
伊藤忠テクノソリューションズ、NECソリューションイノベータ、NTTコミュニケーションズ、NTTドコモ、Google、コムチュア、第一生命情報システム、東京海上日動システムズ、日本IBM、BIPROGY、富士ソフト、富士通、三菱UFJインフォメーションテクノロジー、ヤフー -
[教育・学習支援業]
神奈川県公立高等学校、東京都公立高等学校、広島県公立高等学校、福島県公立高等学校、北海道公立高等学校、埼玉県公立中学校、千葉県公立中学校、東京都公立中学校、私立中学校・高等学校 -
[サービス業]
NTTロジスコ、シミック、東洋信号通信社
2021年3月~2023年3月卒業生
- ■伊藤 研究室
-
[専攻]解析学 [指導教員]伊藤 弘道 教授 [キーワード]偏微分方程式論
[テーマ例]❶滑らかでない領域における偏微分方程式の解の性質 ❷非破壊検査に関わる逆問題 ❸地震学における特異型積分方程式の解の構成身の回りで起きているさまざまな現象(自然現象など)の数学解析が本研究室のテーマです。現象を数学的に記述しようとすると多くの場合、微分方程式が現れます。その微分方程式を解析することにより、現象を理解・解明したいと考えています。特に、固体材料に関する現象(地震、破壊現象など)の数学解析とその応用として材料の安全性を調べる非破壊検査に関わる逆問題について研究しています。ゼミでは極力、学生の興味に応じてテーマを設定し、微分方程式の物理的背景やそれを解くための基礎理論を研究します。
- ■遠藤 研究室
-
[専攻]代数学 [指導教員]遠藤 直樹 講師 [キーワード]可換環論
[テーマ例]❶Blow-up代数の環構造論 ❷ホモロジー代数を用いた局所環の構造論可換環論とは,数や函数などの集合のように,加減乗除という四則のうち加減乗を自由に行うことができる「世界」の構造を,主にこれら3つの演算を手掛かりに統一的に理解し,解析しようとする数学です。現在では,代数幾何学や特異点論,整数論,組合せ論,表現論などと密接に関連した複合分野となっていて,これら諸分野における基本言語の1つでもあります。本研究室では,イデアル論を駆使した環の内部構造解析を行っています。
- ■小谷 研究室
-
[専攻]離散数学 [指導教員]小谷 佳子 教授 [キーワード]グラフ理論
[テーマ例]❶グラフの因子グラフ理論は有限集合の2元部分集合について研究する離散数学の1分野です。「どんな地図でも4色以下で塗り分けることができる」という四色定理はグラフ理論の有名な定理の一つです。本研究室では、グラフ理論の中の因子論、特に正則因子が存在するための十分条件について研究しています。
- ■齊藤 研究室
-
[専攻]関数解析学 [指導教員]齊藤 功 准教授 [キーワード]作用素論
[テーマ例]❶ヒルベルト空間上の作用素について関数解析学では個々の関数について調べるというよりも、関数の集まりの空間(関数空間)や、関数空間を抽象化した空間、そしてそれらの空間上の作用素について研究します。微分や積分も関数空間上での作用素として捉えることができます。さまざまな作用素の中で最も扱いやすいものとして正規作用素がありますが、それを基本として、さらに一般的な作用素について研究します。
- ■■佐古 研究室
-
[専攻]数理物理学、幾何学、教育数学 [指導教員]佐古 彰史 教授 [キーワード]整数論
[テーマ例]❶ゲージ理論、弦理論の微分幾何学 ❷ゲージ理論、弦理論を用いた位相幾何学 ❸数学教育法すべての基礎物理理論は、ゲージ理論という微分幾何学の理論で記述されます。数学と物理は車の両輪のように互いに発展し、一般相対性理論とリーマン幾何学のような成功例もあれば、場の量子論のように数学的定式化を拒み続けている例もあります。本研究室では、場の理論や弦理論といった物理理論の数学的な側面や、新しい数学の可能性について研究しています。また数学教育の研究も行っており、数学的側面からのアプローチも試みています。教育方法から、教育を数学的に考察するなど発想は自由です。
- ■佐藤 研究室
-
[専攻]代数学、位相幾何学 [指導教員]佐藤 隆夫 教授 [キーワード]組み合わせ群論,群のコホモロジー論
[テーマ例]❶ねじれ係数コホモロジー群の構造 ❷Johnson準同型写像の余核 ❸自由群のSL(m,C)表現環の構造本研究室では、「自由群の自己同型群」や「曲面の写像類群」と呼ばれる群(群とは、掛け算や足し算などの演算を持つ集合のことです)の構造を研究しています。位相幾何学では、直感的な幾何学的現象を厳密に数式で記述するために、かなり高度な代数学を用います。本研究室は、基本群やホモロジー群とよばれる道具(この「道具」を理解するだけでも数年は要するでしょう)を用いて、写像類群の代数的な構造を調べています。
- ■下川 研究室
-
[専攻]統計学 [指導教員]下川 朝有 講師 [キーワード]統計学,機械学習
[テーマ例]❶医療データ解析 ❷生存時間解析 ❸木構造モデル ❹SAS、Rを用いた統計解析 ❺MATLAB、Pythonを用いた機械学習本研究室では数理統計学から実際のデータ解析まで、幅広く統計学に係る研究を行っています。特に臨床試験など医学研究におけるデータの統計解析、また機械学習を用いたパターン認識や予測モデルの構築、そしてその応用に力を入れています。
- ■新田 研究室
-
[専攻]幾何学 [指導教員]新田 泰文 講師 [キーワード]微分幾何学,複素幾何学
[テーマ例]❶リーマン多様体の微分幾何学 ❷代複素多様体の微分幾何学と複素解析幾何学曲線や曲面の一般化である、多様体と呼ばれる空間の幾何学を研究しています。特に、その「曲がり方」に注目して多様体を調べています。本研究室では主に複素関数論に由来する多様体を考え、その複素解析的な性質と「曲がり方」の様子を結びつけて研究を行います。
- ■宮岡 研究室
-
[専攻]統計学 [指導教員]宮岡 悦良 教授 [キーワード]統計学,データ解析
[テーマ例]❶医薬データ解析 時系列解析 ❸Mathematicaによる数理科学 ❹SASによるデータ解析 ❺応用確率論(1)時間とともに移り変わる確率現象の数理モデルとその推測法の研究 (2)臨床試験など医学統計分野におけるデータ解析 (3)コンピュータによるパターン認識の統計的方法とその応用。