ニュース&イベント NEWS & EVENTS
全結合型イジングマシンLSIシステム、容量と精度のデュアルスケーラブル化に成功
~社会のあらゆる組合せ最適化問題に挑む~
研究の要旨とポイント
- クラウドと異なり、エッジ環境では電力や設置形態に制約があるため、問題の特性に応じて容量(スピン数)と精度(相互作用ビット幅)を最適化することが重要です。
- 今回、容量と精度の両方向に展開できる画期的なデュアルスケーラブル全結合型イジングマシンLSIシステムを開発しました。
- 4ビット512スピンLSIチップを複数個用い、それを1つのFPGAで制御することで、10ビット2048スピンおよび37ビット1024スピンに展開した実機検証に成功しました。
- 本技術は、同一のLSIチップ複数個を用いることで、精度と容量の2軸に対して、いずれの方向にも柔軟に展開できる技術です。
研究の概要
東京理科大学 工学部 電気工学科の河原 尊之教授らの研究グループは、同一のLSIチップを複数個用い、それらを1つのFPGA(*1)で統合して制御することで、容量と精度の2軸のいずれの方向にも柔軟に拡張・展開可能な「デュアルスケーラブル全結合型イジングマシンLSIシステム」を開発しました。この技術により、エッジ側でも大規模な組合せ最適化問題(*2)の高速・低消費電力処理が可能となり、社会全体に広がる複雑な組合せ問題の迅速な解決が期待されます。
交通経路や物流、通信ネットワーク、金融、創薬など、組合せ最適化問題は社会のさまざまな場面に存在します。従来の総当たり方式では、候補数の増加に伴い計算量が爆発的に増大し、現実的な解決が困難です。この課題に対し、高速かつ低消費電力で解を探索できる全結合型イジングマシンの活用が注目されています。特にエッジ環境での利用には、使用できる電力や設置環境の面で制約が生じるため、容量と精度の柔軟な拡張性が求められています。そこで今回、そのニーズに応えるため、新たな全結合型イジングマシンのデュアルスケーラブル化に挑戦しました。
本研究では、2種類のデュアルスケーラブル全結合型イジングマシン(DSAPS#1: 2048スピン10ビット、DSAPS#2: 1024スピン37ビット)を開発し、性能の検証を行いました。MAX-CUT問題では、DSAPS#1とDSAPS#2のいずれも、最良解と比較して99%以上の精度を達成しました。一方、ナップサック問題では、DSAPS#2のみ正しい解を得ることができました。これにより、解く問題の特性に応じて適切なビット幅の選択が重要であることが示唆されました。
さらに、これまでの研究成果を踏まえ、2025年度から東京理科大学 工学部 電気工学科3年生の学生実験で、全結合型イジングマシンのLSI実装が取り入れられます。学生全員が全結合型イジングマシンのFPGA実装および評価を行い、実際のLSIとして動作させます。この機会は、半導体設計技術を体験できる貴重な場となることが期待されます。
本研究成果は、2025年3月21日に国際学術誌「IEEE ACCESS」にオンライン掲載されました。
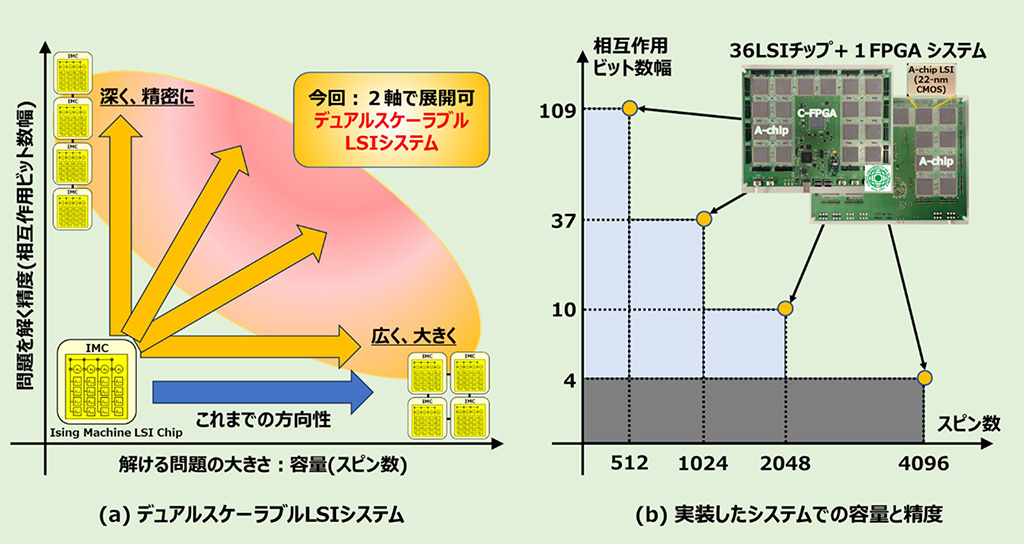
図1. デュアルスケーラブル全結合型イジングマシンLSIシステム
(a) これまで、複数個のLSIチップを統合することで、大きなスピン数を実現する容量方向のスケーラブル化に成功した。今回、複数個のLSIチップを統合することで、大きな相互作用ビット幅を実現する精度方向のスケーラブル化も可能にした。
(b) 36個の512スピン(容量)4ビット(精度)のLSIチップと1個のFPGAを搭載したボードを用いて、容量と精度の両方向に対するデュアルなスケーラブル化を実証した。
研究の背景
-
全結合型イジングマシン
交通経路や物流コストの最適化、通信・電力網の最適化、金融ポートフォリオの決定、創薬や新素材開発など、組合せ最適化問題は社会のあらゆる分野に存在しています。しかし、これらの問題を総当たりで解く方法では、候補数(例えば、物流の配送先数)が増えると、必要な時間(計算量)が指数関数的に増加してしまうため、実用的ではありません。そのため、全結合型イジングマシンによる解決が期待されています。
イジングマシンでは、組合せに対応するスピンσi(+1あるいは-1の二値)と、組合せの実現しやすさ・しにくさに対応する結合Jij(相互作用: ビット幅が大きいほど、より細かな差を表現できる)を用います。全結合型イジングマシンでは、各スピンσiとσjのすべての間に結合Jijが存在することを考慮するため、組合せ最適化問題はこのJijの組に変換することができます。そして、このJijに基づいて計算した全結合型イジングマシンのエネルギーが最小となるスピン配置が、組合せ最適化問題における最適解に対応します。
組合せの重要度や影響力に対応するhiを含めると、このエネルギーEは下記の(式1)で表すことができます。
E=-∑(i,j)Jijσiσj−∑ihiσi(式1)
このσiの変化を定めるエネルギーEiは、下記の(式2)で表すことができます。
Ei=-σi (∑jJijσj+hi )
=−σi (ΔEi + hi)(式2)
(式2)を全てのスピンで足し合わせると(式1)となります。ホップフィールドは、σiの変化がΔEi + hiの符号によって決まるとしたホップフィールドネットワーク(*3)を提案し、これを用いることで、組合せ最適化問題が解けることを示しました。しかし、局所的に小さな値(局所解)で変化が止まってしまう場合があることが判明したため、ΔEi + hiの値に基づいて確率的にσiが決まるように改良されました。これが、アニーリング機構を備えた全結合型イジングマシンで、広義にはボルツマンマシンとして説明されます。
解を求めるには、スピン値と結合値の積和であるΔEiの計算が重要です。大規模な組合せ最適化問題ではより多くの組合せを扱うため、最適化対象の組合せの数、つまりスピン数の拡張が必要となります。また(式2)からわかるように、Jijのビット幅を拡張することで、ΔEiを高精度に計算できるようになります。物流の例では、組合せは配送先の数や時間に対応しており、Jijのビット幅が大きいほど、運送時間の差をより細かく表現できることを意味します。Jijのビット幅が大きくなり、ΔEiが高精度になることで、こうした微小な差を考慮した最適解を導くことが可能となります。
一方、エッジ環境では、電力や設置形態に制限があるため、解く問題に応じて容量(スピン数)と精度(相互作用ビット幅)を柔軟に調整できることが求められます。また、その設定が容易に切り替えできる仕組みも求められています。
-
スケーラブル全結合型イジングマシン
大規模な組合せ最適化問題では、必然的にスピン数が増加します。Jijはこのスピン数の二乗に比例するため、その個数は非常に多くなります。このため、大規模な問題を扱う際には、このJijの個数の増加が大きな課題となります。近年の半導体技術では微細化が進んでいますが、微細化だけで対応するのには、コスト面も含めて限界があります。そこで、複数のLSIで計算を分割し、それらを統合することで対応するスケーラブル全結合型イジングマシンが発展してきました。
具体例として、4個のLSIチップとこれらを統合する1つのFPGAを用いる構成を考えます。スケーラブル全結合型イジングマシンでは、ΔEiの計算を4つに分割しており、以下の(式3)で求めることができます。
ΔEi = ΔEi1 + ΔEi2 + ΔEi3 + ΔEi4(式3)
つまり、4つのLSIで別々に対応する項を計算し、1つのFPGAでそれらを足し合わせてΔEiを求めれば、全結合型イジングマシンの動作を実現することができます。これが、スケーラブル全結合型イジングマシンの原理です。
-
デュアルスケーラブル全結合型イジングマシン
今回、スケーラブル全結合型イジングマシンを基に、規模の拡張だけでなく、計算精度であるJijのビット幅についてもスケーラブルに対応できる構成を実現しました。ここで、ΔEiは以下の(式4)で表されます。
ΔEi = ∑j Jij σj(式4)
例として、各LSIのJijのビット幅を符号付き4ビットとします。従来のスケーラブル全結合型イジングマシンでは、この4ビットのまま、LSIの個数を増やす方法を取っていました。今回の新提案では、統合する1つのFPGAでLSIチップ4個からのエネルギーの和を計算するときに、単純に足し合わせるのではなく、事前にビットシフトを行います。この時の和をΔEihとすると、以下のように表すことができます。
ΔEih = 20·ΔEi1 + 23·ΔEi2 + 26·ΔEi3 + 29·ΔEi4(式5)
これを(式4)と合わせて考えると、各LSIから出力されるJijにビットシフトを適用して、それを統合することで、Jhijを実現していることと等価となります。各LSIのJijのビット幅は符号付き4ビットで、これを3ビットずつシフトして足し合わせることで、統合後のJhijは符号付き13ビットとなります。これは符号付き13ビットのJhijを、符号は共通のまま、4つのLSIチップに対して、3ビットずつ桁を区切って入れたことになり、より大きなビット幅を用いて結合を表現できることを意味します。
このようにすることで、計算精度を決めるJijのビット幅をスケーラブルに拡張することができます。この場合、容量については元のLSI構成のままとなります。この(式5)による精度方向の拡張手法は、(式3)で示した容量方向の拡張手法と同様に非常に単純です。そのため、FPGA側の処理負荷もごくわずかで、ビットシフトを行うかどうかの違いだけとなります。さらに、ビットシフトを行わない容量方向の和と、今回のビットシフトを行うことで実現する精度方向の和は、取り扱うLSIの総数に制限はありますが、それぞれ独立に設定することが可能です。そのため、用途や目的に応じて両者を併用し、デュアルにスケーラブルな構成を実現することができます。
研究結果の詳細
-
デュアルスケーラブル全結合型イジングマシンの開発と検証
これまでに報告したスケーラブル全結合型イジングマシンボードを基に、今回、新たに2種類のデュアルスケーラブル全結合型イジングマシン(DSAPS#1とDSAPS#2)を開発しました。このボードは、36個のLSIチップ(1チップあたり4ビット512スピン)と1つのFPGAで構成されています。DSAPS#1では、30個のLSIチップを10個ずつ3組のグループに分けて使用し、各グループで2048スピンを実現しました。また、この3組のグループを用いることで、10ビットのビット幅を実現しました。DSAPS#2では、36個のLSIチップについて、3個のLSIチップで1024スピンを構成し、これを12組用いることで、37ビットのビット幅を実現しました。
2種類のデュアルスケーラブル全結合型イジングマシンを用いて、MAX-CUT問題とナップサック問題を解いて検証を行いました。MAX-CUT問題では、DSAPS#1とDSAPS#2のいずれも、別途厳密に解いた最良解と比較して、99%以上の精度を達成しました。一方、ナップサック問題では、DSAPS#2では正しい解を得ることができましたが、DSAPS#1では正解との乖離が大きくなりました。これらの結果は、解くべき問題の特性に応じて、適切なビット幅を選択することが重要であることを示唆しています。
-
教育展開(全結合型イジングマシンのLSI実装)
全結合型イジングマシンのエッジ側でのLSI実装について、東京理科大学 工学部 電気工学科では、2015年の開始以来、10年以上継続的かつ系統的に研究を推進してきました。2016年、国際学会IEEE NEWCASにおいて、全結合型LSI構成を提案したことを皮切りに、2020年には単一チップに全結合型イジングマシンを実装することに成功し、さらに、2022年3月および2024年1月にはスケーラブル構造を提案・実証しました。そして今回、デュアルスケーラブルな全結合型イジングマシンへと発展させることに成功しました。
このような進展の中、2025年度からは教育の一環として、東京理科大学 工学部 電気工学科3年生の必修科目である学生実験に、全結合型イジングマシンのLSI実装を取り入れることとなりました。実験テーマの1つとして、基本的な全結合型イジングマシンのFPGA実装および評価を行う内容が組み込まれています。今後、電気工学科3年生全員が、全結合型イジングマシンという1つのまとまった機能を実現する集積回路を、FPGAを用いて設計・実装し、実際のLSIとして動作させることとなります。これは近年、強化が求められている半導体設計技術の良い学びの機会となります。実験の内容については、公開されているシラバスで確認することができます。
下記URL先のページで授業科目「電気工学実験2」を検索。
https://www.tus.ac.jp/academics/degree/syllabus/下記は、現在公開中のシラバスの内容(なお、シラバスは適宜改訂される)。
3. イジングマシンのFPGA実装および評価
<1>社会の至る所に存在する組合せ最適化問題を解くイジングマシンのMATLABを用いたシミュレーション、およびVerilog HDLの演習を行う。
<2>Verilog HDLを用いたイジングマシンのFPGA実装、および実機検証を行い、シミュレーションと比較しハードウェア化による性能向上の理解を深める。※本研究は、日本学術振興会(JSPS)の科研費(23K22829, 25K07849)の助成を受けて実施したものです。
用語
*1 FPGA
Field Programmable Gate Arrayの略。予め用意された論理回路の組合せを製造後に変えることができ、所望の機能を実現できるLSI(半導体集積回路)。
*2 組合せ最適化問題
選べる組合せの中から、与えられた条件を満たす一番良いものを探し出す問題を組合せ最適化問題と呼ぶ。この問題に分類される課題は社会の至る所に広がる。ここで、「与えられた条件」とは、この問題を解くべきとなった活動の目的や戦略を表すことになるため、最適化結果含めて秘匿性の高い内容となる。身近なものでも物流・送電経路探索、倉庫・施設管理最適化、人員・生産計画管理、通信回線最適化、エネルギー貯蔵装置最適配置、金融ポートフォリオ、マーケティングなどがある。
*3 ホップフィールドネットワーク
1972年に甘利によってその原理が、及び1982年にホップフィールドによって応用含めて示された相互に対称に結合したニューラルネットワークである。甘利-ホップフィールドモデルでは、最初ニューロンσiの値は0であったとし、このニューロンに対するネットワークのエネルギーが下がれば1に更新し、そうでなければ0のままとする活性化関数を用いてこのσiを更新する。このモデルによって、1982年の論文ではスピンの内のいくつかが不明の場合にこれを推定させる動作によって連想記憶への応用が示され、1985年の論文では組合せ最適化問題の解を与えることが示された。
論文情報
雑誌名
IEEE ACCESS
論文タイトル
Dual Scalable Annealing Processing System That Scales Number of Spins and Interaction Bit Width Simultaneously
著者
Dong Cui, Taichi Megumi, Akari Endo, and Takayuki Kawahara
DOI
※本論文はオープンアクセスです。自由にダウンロードし、お読みいただけます。
論文発表者
- 崔 棟
- 東京理科大学大学院 工学研究科 電気工学専攻 2024年度修士課程 修了 <筆頭著者>
- 惠 太一
- 東京理科大学大学院 工学研究科 電気工学専攻 2023年度修士課程 修了
- 遠藤 あかり
- 東京理科大学大学院 工学研究科 電気工学専攻 2023年度修士課程 修了
- 河原 尊之
- 東京理科大学 工学部 電気工学科 教授 <責任著者>
関連国際学会
学会名
IEEE 36th International Conference on Microelectronics (ICM 2024)
論文タイトル
Proposal and Validation of a Dual Scalable Annealing Processing System That Simultaneously Scales Capacity and Precision
著者
Dong Cui, Taichi Megumi, Akari Endo, and Takayuki Kawahara
DOI
10.1109/ICM63406.2024.10815759
発表日
2024年12月16日
学会発表者
- 崔 棟
- 東京理科大学大学院 工学研究科 電気工学専攻 2024年度修士課程 修了 <筆頭著者>
- 惠 太一
- 東京理科大学大学院 工学研究科 電気工学専攻 2023年度修士課程 修了
- 遠藤 あかり
- 東京理科大学大学院 工学研究科 電気工学専攻 2023年度修士課程 修了
- 河原 尊之
- 東京理科大学 工学部 電気工学科 教授 <責任著者>
関連書籍
「人工知能チップ回路入門」(河原 尊之 著、コロナ社、2024年10月刊行)
第7章と第8章で全結合型イジングマシンと関連技術を解説。
