ニュース&イベント NEWS & EVENTS
カオス応答を示すシンプルな系「ベルヌーイシフト写像」の実装・汎用化に大きく前進
~疑似乱数生成など数値シミュレーション技術の発展に寄与~
研究の要旨とポイント
- カオス(※1)を生み出す力学系の代表例であるベルヌーイシフト写像(※2)は、コンピュータなどの2進システムで実装すると、出力値が収束してしまい、カオス的挙動が見られなくなることが課題でした。
- 本研究では、出力を長周期化するために状態値に摂動を与える際に、どのような大きさの摂動を与えるべきかに関する理論的な最良値を得ることに成功しました。
- 本研究をさらに発展させることで、暗号生成、数値シミュレーションなどさまざまな分野への貢献が期待されます。
東京理科大学工学部情報工学科の池口徹教授、筑波大学システム情報系の鮏川矩義助教(元、東京理科大学工学部情報工学科助教)の研究グループは、ベルヌーイシフト写像により生じるカオスの振る舞いについて、摂動法、モジュラ計算(※3)を利用した解析を行い、主要なパラメータの理論上の最良値リストを得ることに成功しました。
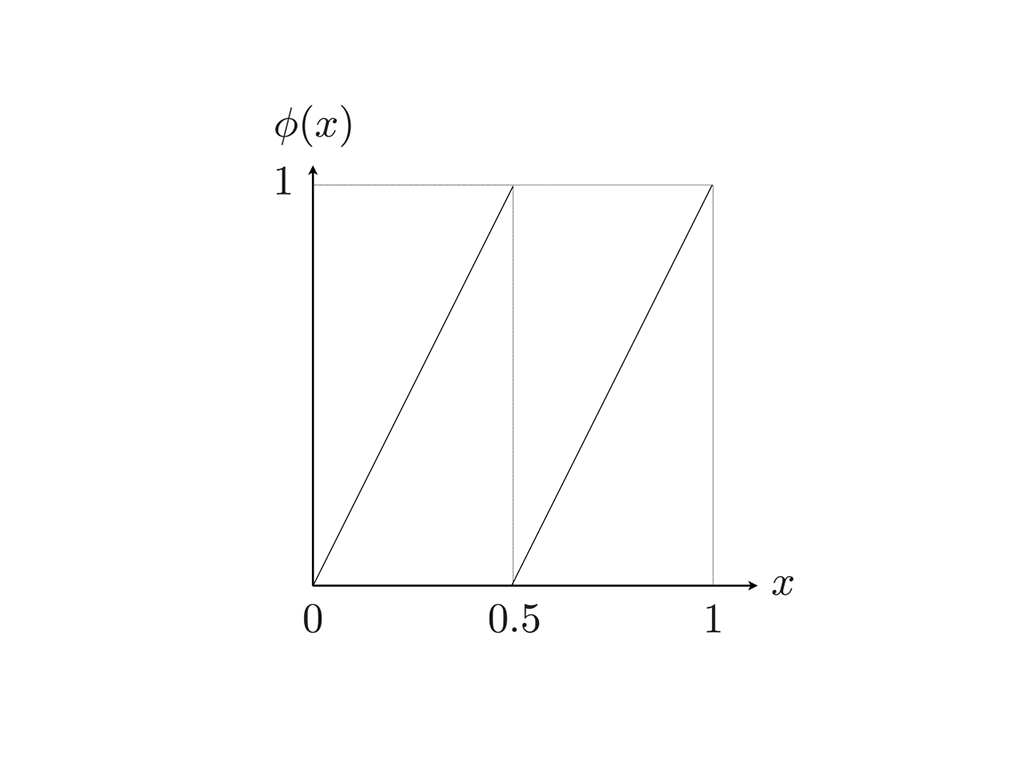
ベルヌーイシフト写像(図1)はカオスを示すことが知られており、アルゴリズム設計、データ解析などに活用されています。しかしながら、コンピュータなどの2進法を基盤としたシステムにこの写像を実装すると、カオスの挙動が見られず、数値が収束してしまうことが課題でした。これを解決するために、本研究グループは摂動法とモジュラ計算を駆使し、得られる数値の周期性に着目して解析を行い、この手法の支配的なパラメータの最良値の網羅的なリストを得ることができました。
本研究では、得られた最良値に対して理論的な裏付けを付与することに成功しています。そのため、ベルヌーイシフト写像を実装する上で役立つことはもちろん、カオスをより深く理解する上でも重要な知見といえます。本成果は、疑似乱数生成、暗号生成や数値シミュレーションなど広い分野での応用が期待されます。
本研究成果は、2022年10月21日に国際学術誌「Chaos, Solitons & Fractals」にオンライン掲載されました。
研究の背景
気象、生命活動、経済など私たちの身の回りにはカオスと呼ばれる現象が多く存在しています。カオスを示す写像の代表例の1つであるベルヌーイシフト写像は非常にシンプルな式で表現され、実装が容易であることが知られています。しかしながら、コンピュータなどの2進法を基盤とするシステムでは、有限精度の初期値を用いる必要があるため、その出力がカオス的な振る舞いにならず、最終的には数値が0に収束するという課題がありました。そこで本研究では、ベルヌーイシフト写像の状態値に摂動を与え、モジュラ計算を適応してこの摂動法で得られる周期の振る舞いを解析すると同時に、プログラムの実装に有用な最良値を得ることを目的としました。
研究結果の詳細
本研究グループは、1未満の正のnビット2進小数εを状態に与える摂動の主要なパラメータとして組み込み、解析を行いました(図2)。
ベルヌーイシフト写像を実装する際には、指定されるビット長はそれぞれ異なります。それぞれのビット長によってεの最良値は異なるので、ビット長ごとの最良値を、モジュラ計算から算出しました。そして、εが最良値となる周期を解析し、その周期が理論的な上限値にかなり近くなることを実際に確認することで、理論的な最良値をリスト化することに成功しました。
この手法の特筆すべき点として、整数論の主要な未解決問題である「原始根に関するArtinの予想(※4)」が真であれば、どんなビット長でも高い性能を維持することが理論的に保証される点が挙げられます。すなわち、この手法は理論的な裏付けが得られているアプローチということができます。
本研究成果は、ベルヌーイシフト写像のプログラム実装だけでなく、他のカオス力学系への応用が期待される有用な知見といえます。本研究の成果について、研究を主導した池口教授は「カオス力学系は決定論的なシステムであるにも関わらず、その非線形性によって複雑な振舞いを示すことから、コンピュータ内での疑似乱数の生成などに使用されています。本研究では、これらに理論的な裏付けを与えることができたといえるので、より応用的な分野にも影響を与えると考えています」と話しています。
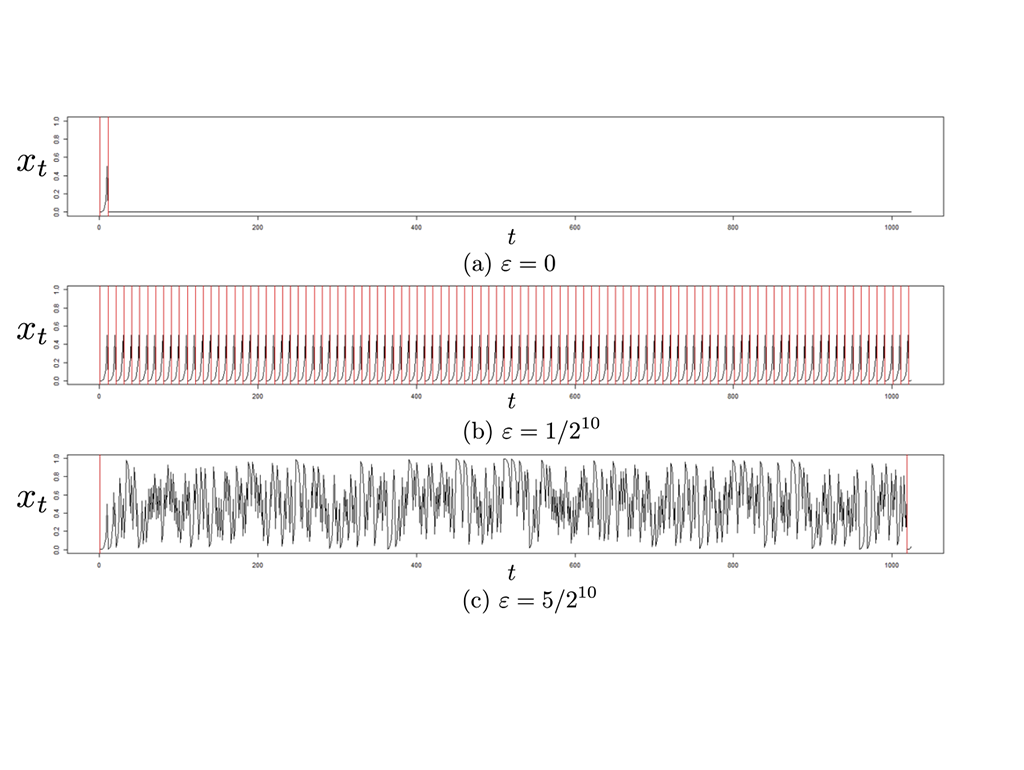
図2. ビット長が10の場合の提案法を用いた結果の例。赤線は周期を表す。
(a) 摂動を与えずに (ε = 0) 実装すると0に収束してしまう。
(b) 摂動の大きさが十分でないと (ε = 1/210) 周期的となる。
(c) 本研究での提案法を用いて摂動の大きさ ε を 5/210 とすると収束しないことがわかる。
※本研究は日本学術振興会の科研費(JP20K19747, JP20H00596, JP21H03514, JP22K18419)の助成を受けて実施されました。
用語
※1 カオス: 決定論的非線形力学系(現在の状態が決まれば、未来の状態も一意に決まる)に見られる不規則で複雑な現象。
※2 ベルヌーイシフト写像: 傾きが2の線形写像を組み合わせた決定論的非線形力学系。
※3 モジュラ計算: 合同算術。ある数をもう一方の数で割ったときの余りに着目し、問題を解く方法。
※4 原始根に関するArtinの予想: 「整数 aに対して、aが -1もしくは平方数でなければ、aを原子根に持つ素数pの集合をS(a)としたとき、(i) S(a) は素数の集合内で正の漸近密度を持ち(したがって、S(a) は無限であり)、(ii) aが累乗数でなく、4を法として1と合同でない場合、その密度はaに寄らない約0.37の定数(Artin定数)となる」という命題が正しいという予想。
論文情報
雑誌名
Chaos, Solitons & Fractals
論文タイトル
How to Perturb Bernoulli Shift Map
著者
Noriyoshi Sukegawa, Tohru Ikeguchi
