2022.11.02 Wednesday
Perturbing the Bernoulli Shift Map in Binary Systems
Researchers effectively tune the parameters of a perturbation method to preserve chaos in the Bernoulli shift map output
The Bernoulli shift map is a well-known chaotic map in chaos theory. For a binary system, however, the output is not chaotic and converges to zero instead. One way to prevent this is by perturbing the state space of the map. In a new study, researchers explore one such perturbation method to obtain non-converging outputs with long periods and analyze these periods using modular arithmetic, obtaining a complete list of parameter values for optimal perturbations.
Is it possible for a deterministic system to be unpredictable? Although counter-intuitive, the answer is yes. Such systems are called "chaotic systems," which are characterized by sensitive dependence on initial conditions and long-term unpredictability. The behavior of such systems is often described using what is known as a "chaotic map." Chaotic maps finds applications in areas such as algorithm design, data analysis, and numerical simulations.
One well-known example of a chaotic map is the Bernoulli shift map. In practical applications of the Bernoulli shift map, the outputs are often required to have long periods. Strangely enough, however, when the Bernoulli shift map is implemented in a binary system, such as a digital computer, the output sequence is no longer chaotic and instead converges to zero!
To this end, perturbation methods are an effective strategy where a disturbance is applied to the state of the Bernoulli shift map to prevent its output from converging. However, the choice of parameters for obtaining suitable perturbations lacks a theoretical underpinning.
In a recent study made available online on October 21, 2022 and published in Volume 165, Part 1 of the journal Chaos, Solitons & Fractals on December 2022, Professor Tohru Ikeguchi from the Tokyo University of Science in association with Dr. Noriyoshi Sukegawa from University of Tsukuba, both in Japan, have now addressed this issue, laying the theoretical foundations for effective parameter tuning. "While numerical simulations can tell us which values of the parameters can prevent convergence, there is no theoretical background for choosing these values. In this paper, we aimed to investigate the theoretical support behind this choice," explains Prof. Ikeguchi.
Accordingly, the researchers made use of modular arithmetic to tune a dominant parameter in the perturbation method. In particular, they defined the best value for the parameter, which depended on the bit length specified in implementations. The team further analyzed the output period for which the parameter had the best value. Their findings showed that the resulting periods came close to the trivial theoretical upper bounds. Based on this, the researchers obtained a complete list of the best parameter values for a successful implementation of the Bernoulli shift map.
Additionally, an interesting consequence of their investigation was its relation to Artin's conjecture on primitive roots, an open question in number theory. The researchers suggested that, provided Artin's conjecture were true, their approach would be theoretically guaranteed to be effective for any bit length.
Overall, the theoretical foundations put forth in this research are of paramount importance in the practical applications of chaotic maps in general. "A notable advantage of our approach is that it provides a theoretical support to the choice of best parameters. In addition, our analysis can also be partially applied to other chaotic maps, such as the tent map and the logistic map," highlights Dr. Sukegawa.
With distinct advantages, such as simplicity and ease of implementation, the Bernoulli shift maps is highly desirable in several practical applications. And, as this study shows, sometimes chaos is preferable to order!
|
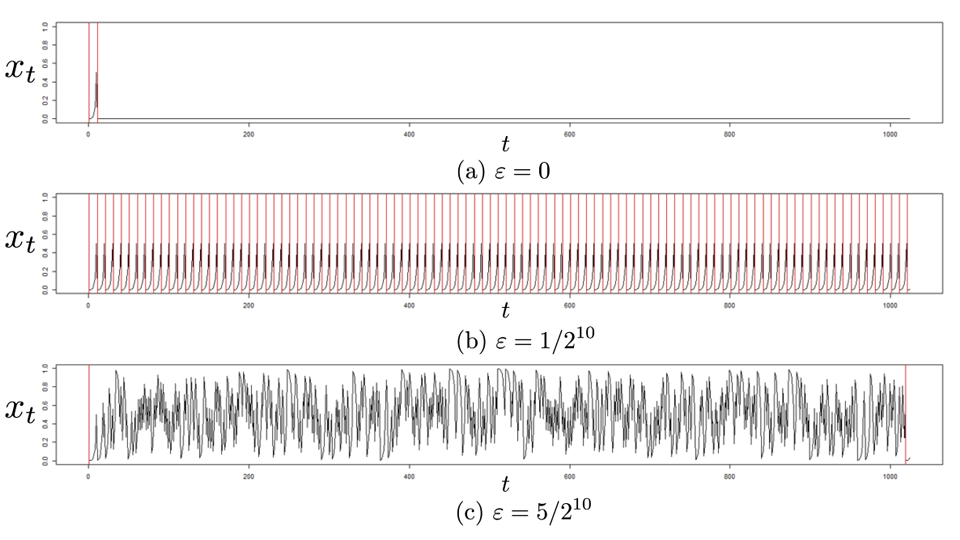
Image title: Examples of results using the proposed method for a bit length of 10. The red line represents the period.
Image caption: Bernoulli shift maps are theoretically chaotic, but produces converging outputs when implemented in binary systems. While this can be avoided by perturbing the map's state space, the parameter tuning for best perturbation has no theoretical basis. Now, researchers from Japan provide this theoretical support underlying the optimal parameter values. (a) If ε = 0 is implemented (no perturbation), the output converges to 0. (b) If the perturbation is not large enough (ε = 1/210), the output becomes periodic. (c) If ε is set to 5/210 using the proposed method in this study, the output does not converge.
Image credit: Prof. Tohru Ikeguchi from TUS and Dr. Noriyoshi Sukegawa from University of Tsukuba, Japan.
License type: Original content
Usage restrictions: Cannot be reused without permission.
Reference
| Title of original paper | : | How to Perturb Bernoulli Shift Map |
| Journal | : | Chaos, Solitons & Fractals |
| DOI | : | 10.1016/j.chaos.2022.112793 |
About The Tokyo University of Science
Tokyo University of Science (TUS) is a well-known and respected university, and the largest science-specialized private research university in Japan, with four campuses in central Tokyo and its suburbs and in Hokkaido. Established in 1881, the university has continually contributed to Japan's development in science through inculcating the love for science in researchers, technicians, and educators.
With a mission of "Creating science and technology for the harmonious development of nature, human beings, and society", TUS has undertaken a wide range of research from basic to applied science. TUS has embraced a multidisciplinary approach to research and undertaken intensive study in some of today's most vital fields. TUS is a meritocracy where the best in science is recognized and nurtured. It is the only private university in Japan that has produced a Nobel Prize winner and the only private university in Asia to produce Nobel Prize winners within the natural sciences field.



About Professor Tohru Ikeguchi from Tokyo University of Science
Tohru Ikeguchi received his B.E., M.E., and D. E. degrees from Tokyo University of Science (TUS), Japan. After working for nearly a decade as a Full Professor at Saitama University, Japan, he joined TUS as a Full Professor at the Department of Management Science and worked there from 2014 to 2016. Since then, he has been a Full Professor at the Department of Information and Computer Technology in TUS. His research interests include nonlinear time series analysis, computational neuroscience, application of chaotic dynamics to solving combinatorial optimization problems, and complex network theory. He has published over 230 papers and proceedings and refereed over 140 papers and proceedings.
Funding information
This study is partially supported by Grant-in-Aid for Early-Career Scientists (no. JP20K19747), Grant-in-Aid Scientific Research (no. JP20H00596 and JP21H03514), and Challenging Research (Pioneering) (no. JP22K18419)

