インストラクターブログ
カルマン渦列(渦列)
こんにちは。学生スタッフのA.S.です。ポスター発表のために勉強した内容をせっかくなのでここにも残しておこうと思います。流体力学における重要なカルマン渦列という現象についてポスターを作成しました。これは「気象庁 カルマン渦」と調べれば観測データが出てくるほど有名な現象です。
カルマン渦列とは、川のような流れのある場所に障害物があるとき、流れが一定の速度を超えると「障害物の後ろに発生する渦の列」のことをいいます。そしてこの渦列には非対称で左右交互に渦が生じる周期性があるという面白い特徴を持ちます(画像は右(青)が先の静止画ですが、このあと左(赤)が前になり、それが繰り返されます)。
流体力学における有名なNavier-Stokes方程式を条件下で無次元化すると出てくるレイノルズ数:Reの値がカルマン渦列の発生に関わっていることが分かっています。
\[\frac{\partial \mathcal{v}'}{\partial t'}+(\mathcal{v}'\cdot\nabla')\mathcal{v}'=-\nabla 'p'+\frac{1}{\mathrm{Re}}\Delta '\mathcal{v}'\]
このReが実験結果と一致しているということもあって方程式の周期解がカルマン渦列に対応していると考えられています。ちなみにRe≈47でカルマン渦が発生することが知られています。これ以上踏み込むとがっつり数学(物理)の世界なので、引き返しますが、自然における現象も数式で記述できるということです。
さて実はカルマン渦列について厳密な数学的解析はまだあまりなされていません。実験結果に支えられている部分が強いのです。理論で語れるように厳密性を追求するのが数学者の役目のひとつなのでしょう。
今回の画像はChatGPTに協力してもらいながら自分で作成したシミュレーションです。この画像もポスターに掲載して一月末にポスター発表をしました。ポスター発表で興味を持ってくださった方々と話していて、自分にはない視点からの疑問などが得られ、さらに調べるのも面白そうだと感じました。
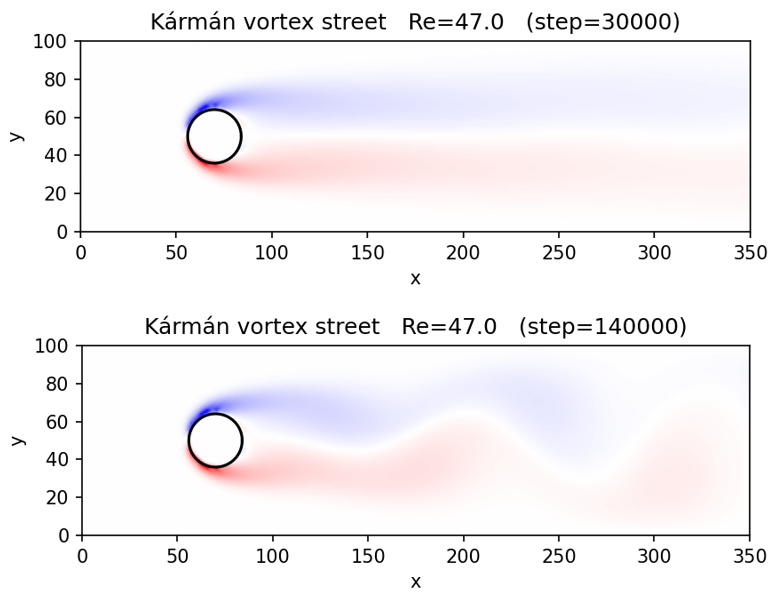
シミュレーション(カルマン渦列発生前、後) ※最後に補足あり

