インストラクターブログ
重力加速度とは
こんにちは。学生スタッフのT.Y.です。近代科学資料館の企画展で取り上げている人物の中村精男は富士山頂で「カーター振り子」を用いて重力加速度を測定しました。今回は「重力加速度とは何か」についてお話ししたいと思います。
まず、重力加速度は簡単に言うと「物体を落としたときに、その物体が重力によって1秒間にどのくらい速くなるのかを表したもの」です。つまり、落とされた物体は空気抵抗を無視すると、重力加速度の分だけ速くなります。では重力とは何でしょうか。図を用いて簡単に説明させていただきます。
ニュートンの万有引力によると、地球上の物体には地球の質量による引力を受けます。さらに、物体には地球の自転による遠心力が働きます。つまり地球上の物体は、地球の内向きに働く引力と外向きに働く遠心力を受けています。そして、この引力と遠心力を合わせた力が重力です。簡単なため、赤道上での物体に働く重力を見積もってみます。まず、赤道上での地球の半径を r 、地球の質量をm 、地球上の物体の質量をM 、万有引力定数をG とすると、地球上の物体に働く引力は
\[F_{引力} = \frac {GMm} {r^2}\]と表されます。次に地球の自転の角速度( 1rad回転するのに何秒かかるか)を𝜔 とすると、赤道上の物体に働く遠心力は
\[F_{遠心力} = m\omega^2r\]と表されます。よって、重力と重力加速度gは
\[F_{重力} = mg = F_{引力} - F_{遠心力} = \frac {GMm} {r^2} - m\omega^2r\] \[g = \frac {GM} {r^2} - \omega^2r\]と求めることができます。この式を見ると、標高が高い場所では地球の半径r が大きくなるため、引力は小さく、遠心力は大きくなり、重力が小さくなることがわかります。つまり、重力加速度も小さくなります。
以上のことから、重力とは「地球上の物体が受ける地球による引力と地球の自転による遠心力を合わせた力」であることがわかります。また、重力加速度は「物体を落としたときに、その物体が重力によって1秒間にどのくらい速くなるのかを表したもの」となります。
ここで、重力加速度にまつわる興味深い話をさせていただきます。ニュートンの運動方程式によると、物体(質点)にかかる力 Fは物体の質量mとその物体の加速度a の積で表せるため
\[ma = F\]となることが知られています。物体を落としたとき、空気抵抗がない(例えば真空中)状況では、物体には重力(質量と重力加速度の積)のみの力が働いているため
\[ma = mg\]となります。そして両辺を物体の質量mで割ると
\[a = g\]となります。これは、物体の質量によらず落とされた物体の1秒当たりの速度の変化は重力加速度 g(地表では約9.8 m/s2)となることを表しています。つまり、真空中であれば質量の小さい羽も質量の大きい鉄球も同じ速度で落ちていくことになります。これは実際にNASAの実験施設「Space Power Facility」において確かめられました
https://www.youtube.com/watch?v=E43-CfukEgsこのように、私たちの日常生活の経験に反するようなことも物理学を用いれば論理的に説明できるのです。
展示会では、重力加速度の測定で一般的に用いられる「ボルダ振り子」を用いて、実際に現在でも理科大の授業で行われている「ボルダ振り子を用いた重力加速度の測定」の学生実験の様子の動画とともに、中村精男が富士山頂で重力加速度を測定した際に用いた「カーター振り子」を3Dプリンターでレプリカ制作したものを展示しています。ぜひお越しいただき、「科学」に対する興味の第一歩にしていただけたらと思います。
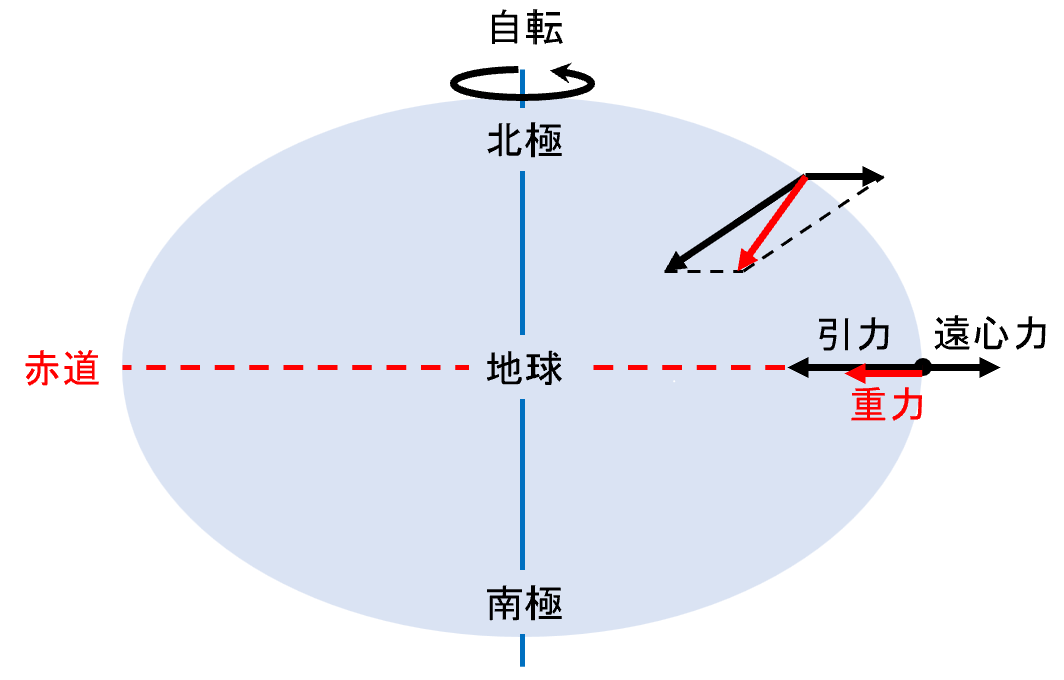
重力の概念図

