Kicking a Soccer Ball

Do you know the shapes that you kick? The surface of a soccer ball is made up of regular pentagons and regular hexagons. Do you know why?

Sliding with Cycloids

Do you know that there are more than one way of how you can design slides? Other than a straight line, you can slide down with curves... With this model of four slides, think, predict and compete about which design of the slide is the fastest and the most fun of them all!

Cutting through A Conic Section

We are surrounded by circles, parabolas, ellipses and hyperbolas. Do you know how they’re made? They are made by slicing a cone in different ways! Can you figure out how it’s sliced and how it got its names?

Manholes and Centers!

Why are manhole covers round? Can’t we have it another way? Find out why they are round and discover much more! You might even be able to create your own manhole cover shape!

Going Crazy with Cradle Pinball!

Imagine a hundred of balls released at one starting point. Which way will they go, left or right? Be amazed as to how these metal balls travel through the metal pins to land in their appropriate columns. Will they be together or will they choose to move away from each other? Discover why!

He loves me… He loves me not… Flower Petal Game

This is a two-player game. Take turns picking one or two adjacent petals off the flower, and the person who picks the last petal wins! Now, see if you can figure out the winning strategy...

Combining a Family of Pentadron Into One

Have you heard of parallelepipeds, skewed hexagonal prisms, truncated octahedra, rhombic dodecahedra and elongated rhombic dodecahedra? They are the five families of parallelohedra. Discover their characteristics and other more figures you can build using these pentadrons!

Reversible Solids: How a Pig Turns into a Ham

You want a ham? Go and rotate that pig. You want your pig back? Go and rotate that ham. Be mesmerized as to how a truncated octahedron, the pig, turns into a ham ... oops, a rectangular prism through the concept of reversible solids.

Spiral Xylophone

Come and listen as a single rolling ball plays you a charming music as it rolls down a spiral xylophone. The steps each have different length, producing different frequencies; hence sounding a beautiful melody.

Can You Draw the Sum of an Infinite Ratio?

How can an infinite number of parts be shown in a figure? It sounds crazy impossible but the sum of an infinite ratio like, (1/4)+(1/4)2+(1/4)3 + … , may be visually shown. Come and see it with your very eyes! By the way, the sum up there is 1/3!

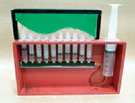
Injecting Areas: Integration Doctor

Be like a doctor and a mathematician while you explore this device which illustrates the concept of integration from area - by approximating the area between a curve and an axis.

Pythagoreans Theorem: From Triangles to Elephants

Maybe you’ve seen this triangle written on a piece of paper. Here, you can explore the relationship of figures and the ever-famous
Pythagorean Theorem in various forms and presentations.

Greatest Common Factor (G.C.F.) and Least Common Multiple (L.C.M.)

Tired of computing G.C.F. and L.C.M. in your head? Play with this device which gives you the G.C.F. and L.C.M. of two natural numbers with just one button! (This is the example shown below,
90=2x3x3x5 and 24=2x2x2x3)

How Much Do You Have in a Watermelon?

Do you know how much you are going to eat if you finish a whole watermelon? Cut through this watermelon and see how cones make up the whole volume of a sphere! Yum!